2012 03/27 筆記対策6～ここまで書いてないこと～

もうだいたい筆記って終わっちゃったのかな？
まぁいいや。
今回は、クレペリンと今までのまとめ的な話をします。


まずクレペリンなんですが、
これは1ケタの足し算を延々とやるもの。
1分×15行×2セットかな。

そのため、根性と腕力が一番重要になります。
ゴールデンウィークに6000ｍ泳いだ後にやらされたときは、
さすがに腕が痛かったですね。笑

これは決して冗談ではないです。

クレペリンは「足し算」をやるものですが、
足し算の能力「だけ」を見てるわけではありません。
※もちろん、速く、正確にできたほうが望ましいのですけど。

具体的には、
「単純な作業を、集中力を切らさずできるかどうか」
がポイントになってたりします。たしか。

だから、
・速く・正確に計算を進める
ことと同時に、
・ある程度イーブンペースを刻んでやる
ことも大事らしいです。
とはいえ、ぴたーっと同じペースだと、
それはそれで作為と判断されちゃうんですけど・・・

結局のところ、
妙な小細工を弄することなく、
最後まで心を折らないように、全力で計算するしかないと思います。

あと、これは厳密には「筆記試験」ではなく「適性検査」です。
つまり、人と比べてどうこう、というよりは、
決められた能力の水準をクリアしているかどうかを見るもの。
なので、そんなに焦らなくていいと思いますよ。



最後なので、筆記対策のまとめ的な話を。

わたくしは、このシリーズをやることで、
飛躍的に解答時間が短縮する、なんて思ってないです。

SPIの中には「推理」とか「図形」とか、
時間をかけて確実に正解を導き出したほうがよさそうな問題もあるので。

そういった問題に時間をさけるようにするために、
他のとこで変に手間取らないでほしい、と思ったのが
このシリーズをやってみたきっかけなのです。
「1問平均○秒でやりましょう」とか
「この問題のポイントはここ！」みたいな
全ての問題に同じようなアプローチしかしない、
対策本に対するアンチテーゼ、とでも申しましょうか。



・・・なんだか、まとめるつもりが逆にまとまらなくなってきました。笑

要は、筆記試験はおそるるに足らず、
ということです！笑

2012 03/07 筆記対策5~たまてばこ~

筆記試験ではSPIって多いですが、
あとテストセンターはSPIですが、
webテストでは、SPIの比率は案外低い。

代わりにシェアをあげてくるのが、GABとか玉手箱とかいうやつ。
よくわかんないけど、たぶん同じです。
図とか表を読み取って、シェアとか伸びとかを計算する。
871はわかるよね？C電のwebテストの形式のこと。

これについては、計算自体は電卓さんに任せてしまえるので、
テクニックもへったくれもない。
ただし電卓ないと撃沈します。絶対終わりません。
ケタ多いし。数字細かいし。
むしろ、ついうっかり無電卓で受けたK社、よく通ったな、オレ・・・

ただし、「表のうち、どこの数字を使用するか」を
いかに速く見極めるかは大事。
最初のうちは、問題文を声に出したり、
指で画面を追いながら探すと、やりやすいかも。

また、最初のうちは1つの計算で済むんですけど、
後半になると、
「以下の選択肢の文のうち、正しいと言えるものはいくつあるか」
などという、うっとうしい問題が登場する。
まぁ5択だったら、たいてい1つはぱっと見で外せますが、
それでもあと4つ。
これは、やらなきゃしょうがない。
後半にこういうものが待っていますから、
前半すいすい行けても、あまり時間に余裕があると思わない方がいいかも。

後は、慣れ。
同じような形式のを3社も受ければ、なんとなく感覚がわかってきます。
5社くらい受ける頃には、時間が余るようになるでしょう。
ただし、慣れるためにマニュアル本使うか―、と思っても、
そううまくはいかない。
マニュアル本にあるような簡単な問題、出ないです。
むしろマニュアル本できたからってなめてかかると、たぶん焦る。



ここまで焦りを増幅するようなことばかり書いてきましたが、
朗報がないわけではない。

この形式、たいてい答えが細かい（割り切れない数値とか）ので、
ほぼ間違いなく、解答は択一式です。
そのため、電卓で計算した数値が選択肢上に存在すれば、
自信を持ってクリックできる。
テストセンターみたいに、疑心暗鬼にとらわれなくてすみます。
あと、小数点の位置を問う問題もちょいちょいあるけど、
そうでない問題も多いので、
桁数のケアレスミスを起こしにくい、というのもポイント。


なんと言っても、「計算の能力」よりは
「表の読解力」のスピードが要求されているので、
そのつもりでやるといいと思います。

2012 02/08 筆記対策４～旅人算

ここは、そんなに難しいことはないと思う。

中学入試だと、「速さ」って結構くせものの単元なんだけど、
SPIじゃそれほどひねた問題も出ないし、
方程式使えるし。

基本的に押さえておきたいのは

「速さ＝距離÷時間」

これだけ。
覚え方は、km/h=km÷h
そう、単位で覚える。
簡単でしょ？

就活本では、まぁ距離を求める式だったり、
時間を求める式も覚えろと書かれていますが、
結局は上の式の変形ですから。
わざわざ、は覚えなくていい、と思う。

とりあえず、問題。
ひっかかる可能性がなくもないひっかけを取り上げます。

【例題１】Aさんが家から分速50mで、学校に向けて歩き出しました。
Aさんが家を出てから6分後に、お母さんが忘れものに気付き、
分速75ｍで追いかけました。
お母さんがAさんに追い付くのは、Aさんが家を出てから何分後か。
また、その地点は家から何m離れているか。

解法：お母さんが家を出るまでに、Aさんが進んだのは50×6＝300m。
お母さんは1分間に、75-50=25(m)ずつAさんとの距離を詰める。
したがって、追い付くのは、300÷25=12（分後）。
ただしこれは「お母さんが家を出てから」。
今回の問題は「Aさんが家を出てから」なので、12＋6=18（分後）が正解。
距離は、50×18=900(m)。
最後の「どこ基準の時間か」の引っかけだけ、案外危ないので要注意。



【例題2】
A船は静水時に15km/h、B船は静水時に12km/hでそれぞれ進む。
今、A船は上流のX地点から下流へ、B船は下流のY地点から上流へ、
それぞれ進み始めた。XY間の距離は72kmである。
川は常に一定の速さＴ(km/h)で流れているものとするとき、
2つの船がすれ違うのは何分後か？

解法：これ、「川の速さが特定できないから答えでない」とか言わないよね？


かたっぽは下り、かたっぽは上ってるんだから、
出会う時間を考える上で、川の速さは相殺されますよ。
出会う地点を考えるなら、マズイですが。

さて。
2つの船の速さの和は27(km/h）。
2地点間の距離は72(km）。
したがって、すれ違うまでには、72/27=8/3（時間）かかる。
で、これを分に直すと、60×8/3＝160（分）。
時間の単位も、気をつけてください。

この分野は、出てくる問題のレベルが高が知れてるんで、
ひっかけにだけ気をつけて、さっさと解くといいと思います。
もっと時間かかるとこ、いっぱいあるからね。

2012 01/30 筆記対策３～食塩水

予告通り久々にやりますシリーズ第3弾。
テストセンターは3月になると埋まるよ、結構。

今回のテーマなんですが、
別に食塩水じゃなくても、
砂糖水でもなんでもいいんですが、
まぁ食塩水がなじみやすいでしょう。
またの名を「濃度算」とかいうやつ。

ほんとはこのテーマ一番やりたかったんだけど、
書くのが面倒なんですよ、図が。

【例題】
5%の食塩水300gと15%の食塩水200ｇを混ぜたら、
混ぜた後の食塩水は何%になるでしょう。

これくらいなら、水溶液の量にパーセントかけて出したって
大した手間ではないのですが。


【例題２】
7%の食塩水160gと18%の食塩水280gを混ぜたら、
混ぜた後の食塩水は何%になるでしょう。

見るからに計算が嫌になりますね。

ここで、「てんびん図」というやつを使います。

てんびんの原則。
「てんびんが釣り合っている場合、
左右の『おもりの重さ×支点からの距離』は同じ」

これを濃度算に応用すると、下の図みたいになる。
即席ペイントだ、お粗末なのは勘弁してください。

さて解法です。

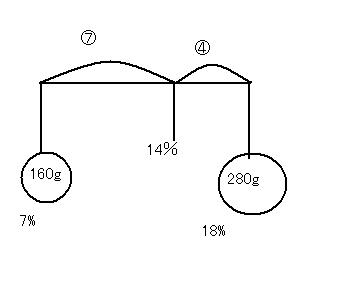7%の食塩水と18%の食塩水の量の比は4:7。
このとき、濃度はこの水の量の逆比をとって動くのね。
つまり、7%から7、18%から4の位置にある濃度になります。
7%から18%までは「11」あるから、
これを7:4に分ける点に注目すると、
これも図に書いた通り、14%。

したがって、答えは14%になります。


嘘だと思ったら、実際に計算してみてください。

つまり、言葉だと説明しにくいんだけど、
「水の量と濃度のパーセンテージは逆比の関係になっている」みたいな。

このやり方の何がいいかって言いますと、
実際の食塩の量を計算しなくてもいいので、
複雑な数値の計算が楽になる、ってのが1つ。

もう1つは、これ1つで2種の濃度算はたいていこなせるということ。

たとえば、こんな問題たちも。
【類題１】5％の食塩水300gに、濃度のわからない食塩水を混ぜたら、
12％の食塩水が900gできました。混ぜた食塩水は何%でしょう。
・・・これは、天秤の片方の重りをxにして、図を書くだけ。

【類題2】15%の食塩水100gをうすめて6%の食塩水を作るには、
真水を何g混ぜればよいでしょう。
・・・こんなときは、水を「濃度0％」の食塩水だと思っててんびん図を書く。

【類題3】7%の食塩水150gに食塩を何gか足して10%の食塩水を作りたい。
加える食塩は何gか。
・・・これ、計算だと結構面倒っすよ。
ただしてんびん図なら、食塩を「濃度100%」の
食塩水だと思っててんびん図を書くだけ。


ね、なかなか役立ちそうでしょ？
これ、問題集だとまったく取り上げてないのですよ。
中学受験だったら必須のアイテムなんだけど・・・

そんなわけで、知らない人は覚えると楽ですよ。

・・・次、何やろう？

2011 12/01 しゅーかつ対策その２ 集合

流行語ベストテンは「こだまでしょうか」か・・・
みんな「おはよウナギ」とか
「ぽぽぽぽーん」のが言ってたよな。

さて、九州の話も残ってますが、
12月1日、就活解禁という日らしいので、
久しぶりに筆記対策をやってみましょう。



今日のテーマは「集合」。

たとえばこんな問題。

〈例題〉
あるクラスの生徒50人を対象に国語と数学のテストをした結果、国語が合格点に達した者は25人、数学が合格点に達した者は30人であった。両科目とも合格点に達しなかった者は6人だった。国語、数学共に合格点に達した者は何人いるか。

〈一般的な解き方〉
よくベン図使えって言われるよね。
こういうやつ。引用はwikiさんより。

これの何がいけないかというと、
というかいけなくはないんだけど、
この後いろいろ数値を書き込むことを考えると、
なかなかキレイな図を書くのが難しい。
しかも時間との勝負だと。


〈オススメの解き方〉
僕はマトリクスを書くのが好き。
○×ゲームみたいなマス目を書くヤツね。
イメージわかない人は、以下のリンクをご覧ください。
http://colorfro.blogspot.com/2011/07/blog-post_19.html

これの何がいいかというと、
さっさっと線を引くだけだから、
書くのが簡単。
あと、表が1つ埋まると、
残りの空白は上下左右の数字から芋づる式にどんどん分かってくるから、
解くのに楽。

今回の問題で言うと、
縦軸に「国語合格」「国語不合格」
横軸に「数学合格」「数学不合格」
ととればOK。
もちろんこんな漢字をつらつらと書く必要もなく、
「こ○」「こ×」程度で十分。
わかりゃいいんだよ、自分だけ。



これが条件3つになると
マトリクスは書きにくいんだけど、
それはベン図も同じ。
特に3つの円が重なるとことか難しいぜ。


ただ実際には、条件が2種類の問題が多いってのと、
条件が3つある大問でも、
そのうちの2つを取ってきてあーだこーだという
小問がほとんどなので、小問ごとに
２×２マトリクスを書けばいいんじゃないかと。

または、２×２マトリクスのマス目を広く取って、
カッコとかで3つ目の条件を書くとか。

まぁ、実際にどっちがいいか試しておくれよ。


最後にちょっとだけ愚痴ると、
就活本では
そらきたベン図、ほら書けベン図ばっかりなんですよね。
まるでベン図以外の解き方がないかのように。
なんで誰もマトリクスに目を向けないのか、が気になる。